This article will describe the preliminary results of our ongoing analysis of the Granite Artefact scan data, released on February 19th, 2023, by the team at unchartedx.com. For an introduction to the object itself, and some more context around how it was digitised, please see the first few paragraphs of my initial analysis.
This article is written by Mark Qvist. The analysis and modelling work required to produce it has been the product of a joint effort between myself, and another engineer. For professional reasons, she currently wishes to remain unnamed. All mentions of "we" in this article refer to us as the authors. Whenever the I pronoun is found, it is used to signify an opinion, observation or conclusion made by myself alone.
Since getting access to the data, we have worked to gain a better understanding of this remarkable object, and we have been making some significant headway.
There is still much to learn, but we would like to share what we know so far. We could in no way have anticipated what came to light in this investigation, and just how extraordinary this object is.
While we cannot yet make any direct conclusions, as to who made this object, or when it was created, we now at least know a great deal more about the capabilities of the creators of the object.
This is a long article. If you want to ascertain wheter it is worth your time, you can skip ahead and read the conclusions first, which I am sure will catch your attention, if it wasn't already focused. If you have the patience though, I will recommend taking everything in its laid out order; there is a lot to unpack here.
We will be using some mathematics to illustrate various points, but we have strived to keep it as simple to follow as possible. With a basic understanding of geometry and algebra, it should be possible to follow most of it. There will be a few sections where the equations get a little more involved. This is necessary to show that our model is valid, but these sections are not essential to the overall understanding of the article.
We will do our best to make the main points stand out even for those not interested in the math and equations. So if those parts doesn't mean anything to you, feel free to skip them.
In this article, we use radians, since it is a universal way to describe angles. Radians are based on the fundamental ratio between the radius and circumference of circle, whereas degrees is just an arbitrary subdivision of a circle into 360 pieces. As such, it is not based on any fundamental mathematical ratios or constants, and not really useful in an analysis such as this. Radians are useful because they show the underlying mathematical relations more clearly.
Radians may lead to some unease, if you are not familiar with them. Fear not, though! It is actually simpler, and much more intuitive than using degrees. All you need to know is that there is $2\times\pi$ radians in a circle, and $\pi$ radians in a triangle. For example, a $45^\circ$ angle is $\pi \over 4$ radians. You can describe any angle by simple fractions of $\pi$.
This section will describe the methodology we employed while working with the object, and offer some context to the choices we made in analysing it, and in our design reconstruction.
Shortly after the scan data of the granite artefact was released, I carried out an initial geometrical analysis of the object. This analysis showed very high levels of geometrical alignment in the object, even between exterior and interior features, as well as specific and consistent choices of angles and dimensional ratios.
These findings very clearly demonstrated, that there was a design behind the finished artefact, and that it did not just randomly appear, out of some intuitively guided fabrication process.
In this article, absolute measurements are given in millimeters ($mm$) or micrometers ($\mu m$), unless otherwise noted. Angles are specified in radians. All measurements mentioned here, have been taken on the high-resolution mesh data from the structured-light scan of the object.
Measurements were made in the application Blender, and parametric CAD models were created using OpenSCAD. The SCAD source code for our model is available for download here. We dimensioned the object in millimeters, and performed measurements by meticulously aligning measurement tools to vertices and polygonal plane intersections. For larger features we measured by manually working towards a best-fit placement of a measurement primitive, by the minimisation of the integral of the amplitudes of deviation over the measured feature.
All graphics and CAD renders presented in this article are ortographic projections. A simulated texture and lighting model has been applied in the renders, to make it easier to visually distinguish curvature and features of the object. This simulated texture is for illustrative purposes, and does not represent the real surface appearance of the object.
The initial findings established the motivation for exploring the object more deeply. The approach taken in this work, has been to attempt to create a mathematically consistent and self-constrained model, that could describe all major features of the physical object.
It has been our theory, that if such a model indeed exists, and can be shown to map well to the actual object, it could allow us to learn a lot more about what processes and principles the designers of the object had access to, and what knowledge they held. By analysing the simplest way to create a satisfactory design for the object, we can get a good idea about the minimum levels of capabilities the designers must have had.
While I am currently the one collating our findings in this article, the work has been a shared effort, and is comprised of the input of a group of people. Without that, we would not have gotten as far in our understanding, as we are now.
When designing an object, be that functional or purely aesthetic, one can take a multitude of approaches. It is of course possible for the designer to simply place various features of an object intuitively, without any underlying rules, constraints or principles, but practically all great design, art and architecture follow sets of internally consistent principles.
Various systems of design principles have been known since antiquity, and when beauty, completeness and harmony in form is experienced, it is often exactly because of the skillfull application of such principles. From the preliminary analysis of the object, we deemed it warranted to investigate whether such a set of principles had been employed in its creation, and if so, to what extent.
An important data point, that can be extracted through this approach, is the degree to which different design patterns are locked together to form constraints. In design work, such constraints are commonly used to define various aspects of the individual features, that make up the finished object.
If we can recreate the object from a relatively simple set of design primitives and constraints, which exhibit low degrees of interrelation, or if indeed no such relations even exist, and all features appear intuitively or randomly placed, this would indicate an object of a relatively low level of design complexity, or one that could have been made entirely from an intuitive process.
Contrarily, if we consistently see features defined by complex interrelations between different principles, this indicates a high level of design complexity, and that a higher level of abstraction was needed; not only in creating the design, but also in transferring it through the production method, to the finished object itself.
To explore what kinds of design principles were used in the creation of the object, we started out by measuring and mapping as many features of the object as possible, and looking for repeating patterns of placement and dimensioning, and repeating or mathematically significant ratios.
While we initially did not understand the underlying principles of what we found, it was clear that patterns and persistent ratios were present in overwhelming abundance throughout the object. Not only were they present, but they exhibited such a high degree of regularity, that we suspected them to be derived from well-defined mathematical formulae.
This led us to attempting something, that really should not have been possible, when dealing with a supposedly ancient artefact, made from granite, of all things: We decided to experimentally build a CAD model that would exclusively use mathematical concepts to dimension and place the features of the object, and use no tuning or arbitrary positional adjustments. All features should be placed and dimensioned by interrelation to each other.
We also limited the initial margin-of-error tolerance of the model to $75~\mu m$, in terms of how well it should map to the features of the actual object. This margin-of-error tolerance was, amongst other criteria, used to discern whether an attempted modelling of a particular feature should be considered for inclusion in the model, or rejected.
I find it timely to stress how completely ludicrous this actually is. We are dealing with a stone vessel of supposed ancient origin, and are now proposing, that a purely mathematical CAD model, should somehow map to the actual object within a tolerance of less than 75 thousands of a millimeter.
Yet, I will let the results speak for themselves. Additionally, the CAD model, and all of its constituent equations, are available for verification, for anyone interested in doing so.
To arrive at a high-level understanding of how the object is defined, we will first look at some primary principles used in the design, and then describe how they are interrelated to create various features of the object.
The most widely used primitive in the object is the circle. Circles, or arcs thereof, are used to define most of the features of the object, and all circular features in the object have radii that are interrelated with incredible consistency and precision.
There is, in fact, one single and elegant equation governing the dimensioning of almost all circles utilised in the design. The few circles not following this pattern have been specifically chosen to display some very significant numbers, which we will get to shortly. But for now, let's look at the radii-determining equation:
With this equation, we can generate all the relevant radii for shaping the object. We can more easily understand how this equation works, by looking at it geometrically.
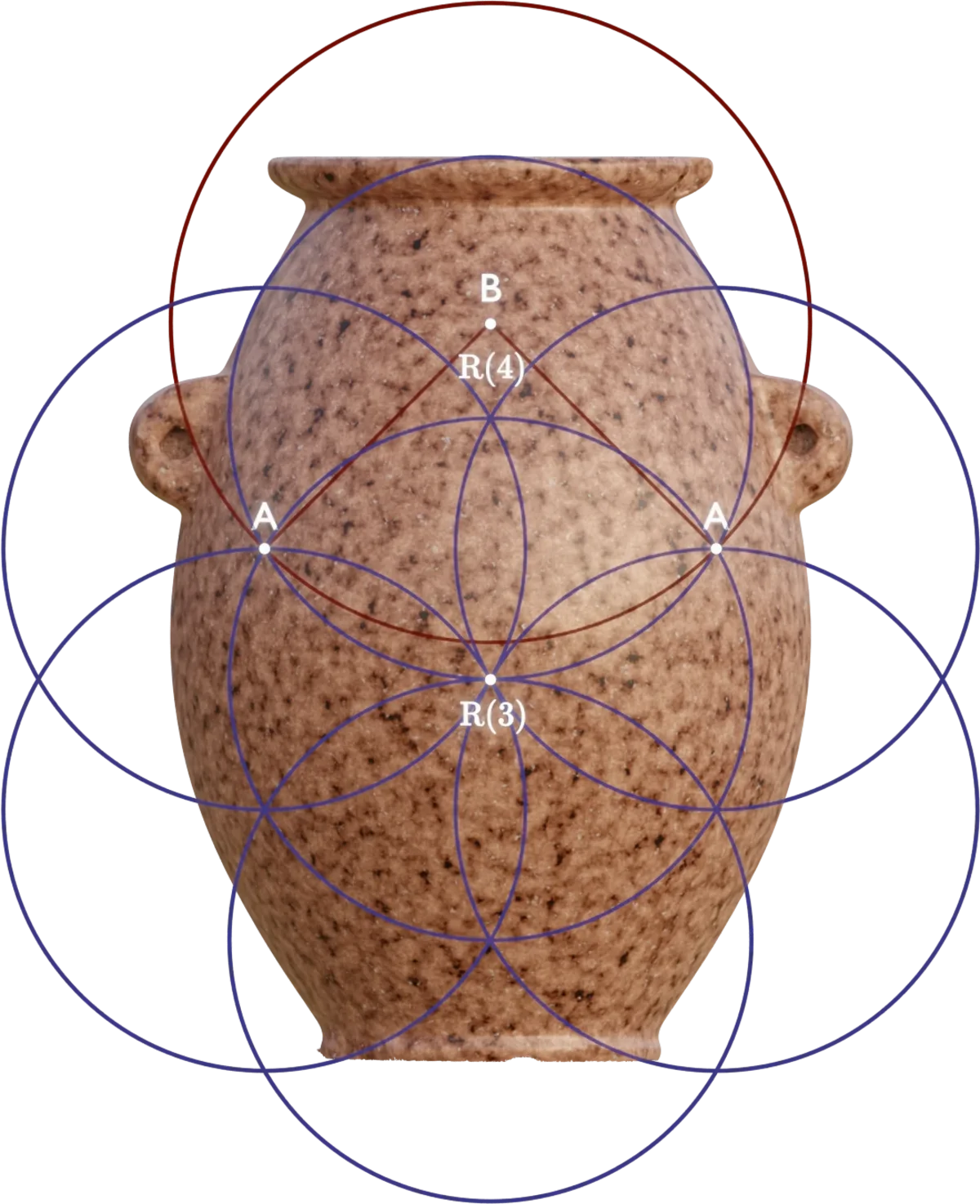
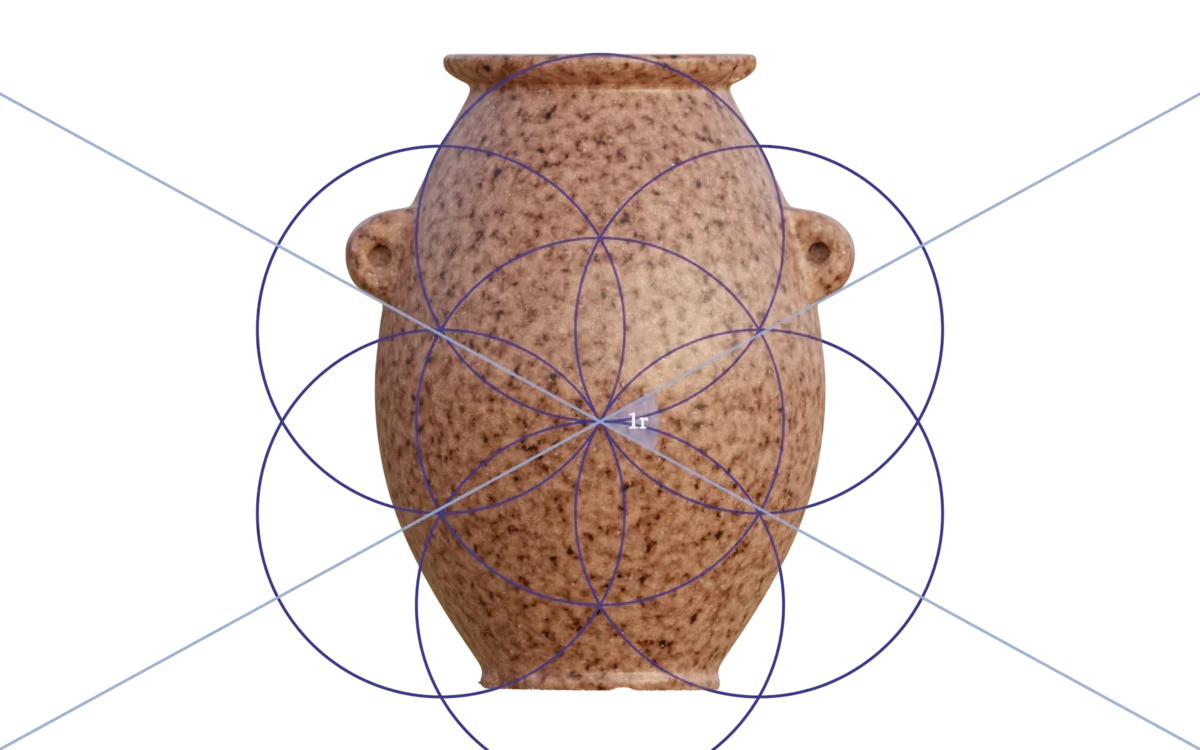
Already in our early investigation, we noticed that many features seemed to be related to a certain geometric construction of unit circles, known as The Flower of Life. We also noticed that not just one, but several, of such grids were used. The above equation is the most simple description of how these grids interrelate to each other.
Let's look at two of these interrelated grids, composed of $R(3)$ and $R(4)$ circles. It is important to note, that there is no arbitrary decisions applied to these grids by us. Both their dimensions and positioning, in relation to each other, are determined by the above equation (and we shall see exactly how shortly). With these two grids, we can already define several features of the object:
The design of the object ascends and descends to and from the various sizes of these Flower of Life grids, by using an elegant geometrical construction:
The ratio between the radii of the two circles is now $\sqrt 6 \over 2$. To clearly see why this is, we can place the following triangles in the construction:
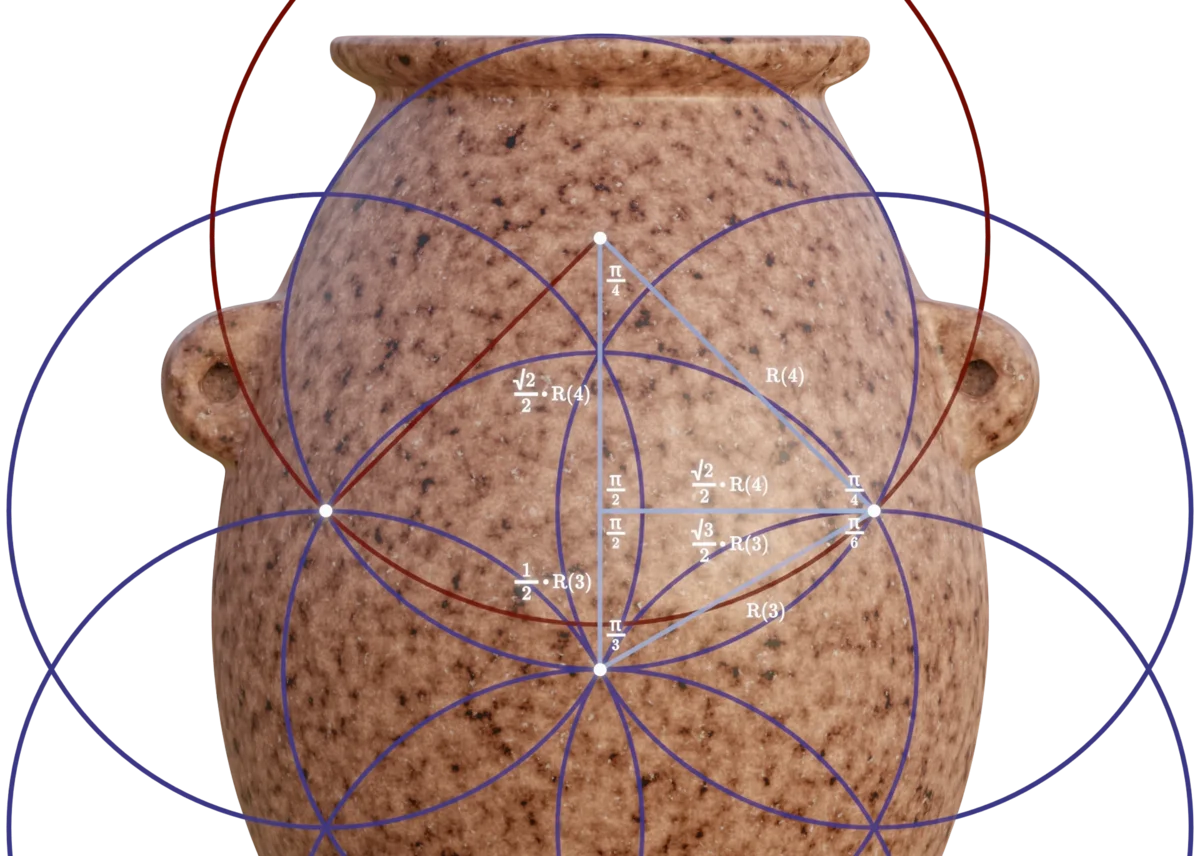
Since these two triangles share one equal side, we can use that to show the ratio:
By the continuation of this pattern, we arrive at the $R(n) = \left({\sqrt 6 \over 2}\right)^n$ function, and thus the radii used in the object can be created:
Since this pattern is used extensively in the object, we will refer to this radial traversal function as $R(n)$ in the rest of this article.
With this elegant construction, we can account for the majority of the circular features in the object. All of the circles created with this function map to the actual radii of the features of the object with incredible precision.
For each of the radii marked in the graphic below, we found the place where the object deviated the most, from the mathematically pure representation of the $R(n) = \left({\sqrt 6 \over 2}\right)^n$ function, and collated these statistics across all observed radii:
Please note, that most radii (even those exhibiting local deviations above the mean) have areas that are, in any meaningful sense of the word, perfect. In many places, the deviation is so small, that we cannot say with certainty whether the deviation is due to "imperfections" in the object, or inaccuracies in the scan. All radii in the following illustration are generated by the $R(n)$ function, and are therefore tightly interrelated:
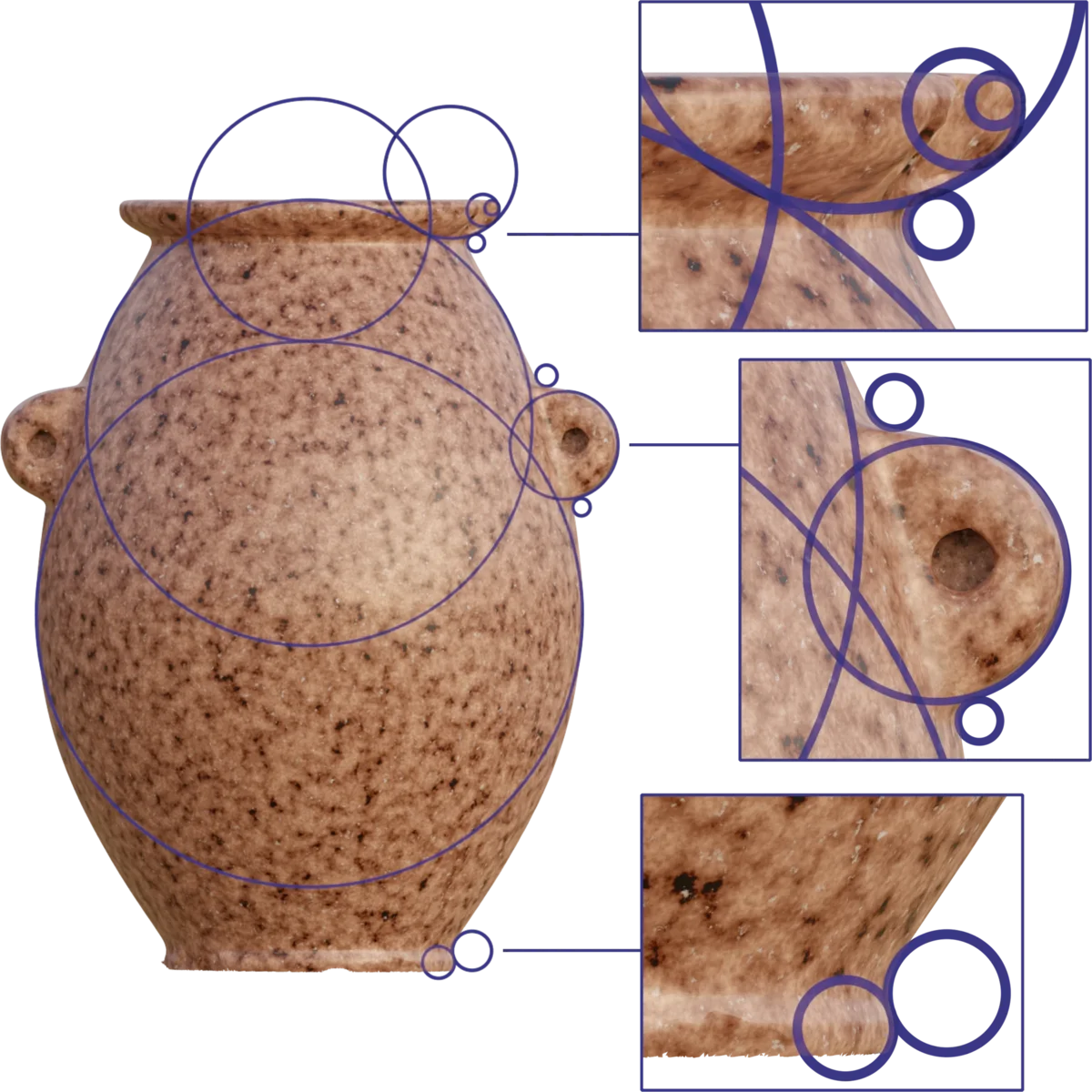
To see this level of consistency of precision across just two or three different radii, created from a purely mathematical function, would be astonishing. To see it completely consistently, to microscopic precision, across $12$ different radii, measuring from just $1.1~mm$, up to $42.2~mm$, in a granite artefact, is more or less unfathomable.
In addition to the radial traversal pattern, we have identified another recurring design principle. The extension of arcs of exactly $1$ radian, locked into configuration with circles created from the radial traversal function, is also used to construct several features of the object.
The part of the body above the handles is composed of two primary regions. The region immediately above the handles exhibits a slight curvature, while the upper region is perfectly conical. This configuration of features can be defined by extending an arc of exactly $1$ radian so that the arc intersects with the $R(3)$ circle defining the maximum extents of the upper body curvature.
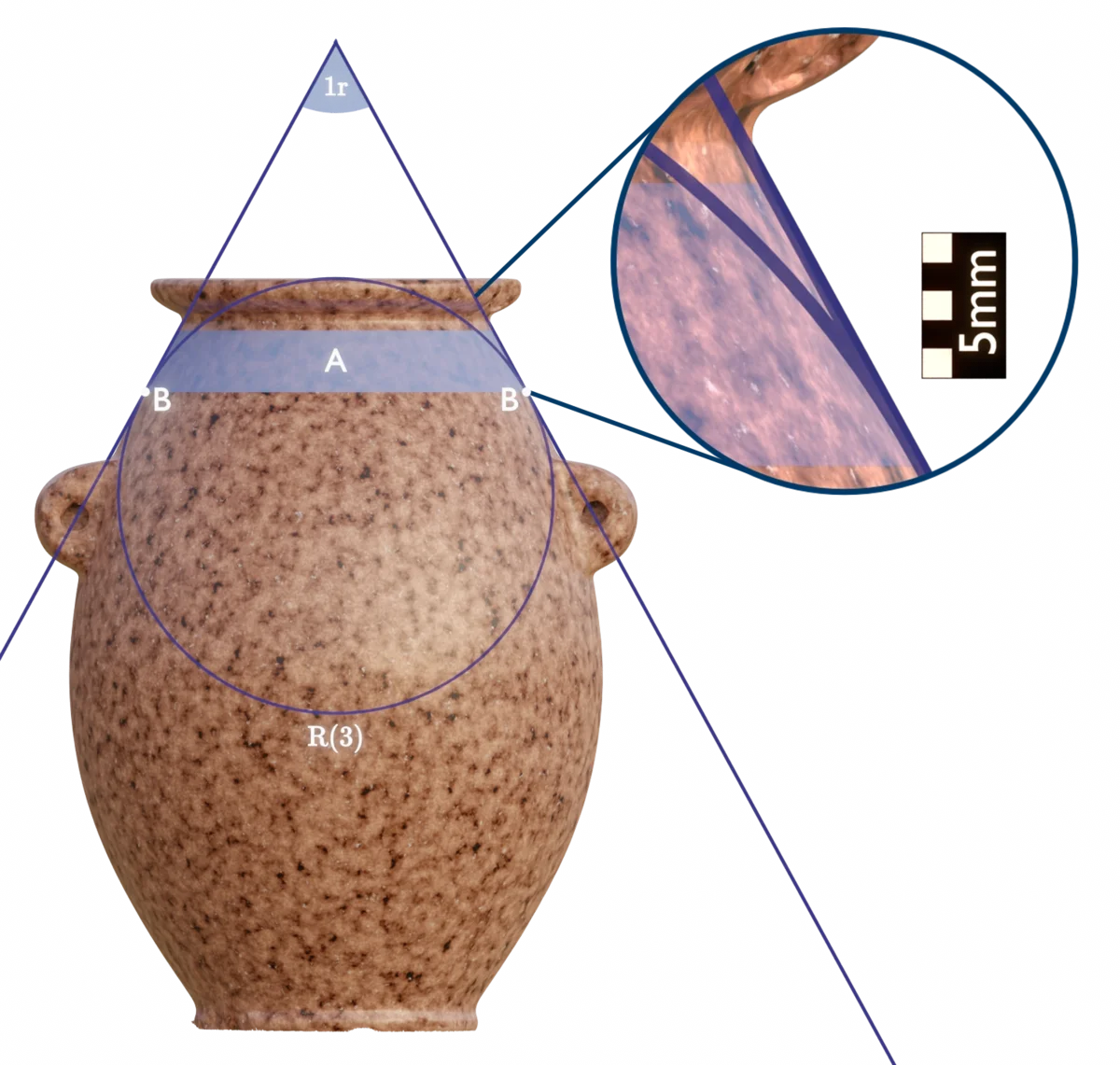
Placing the arc, so that its lines are tangent to the $R(3)$ circle, perfectly maps the conical region (A). And by its intersection with the circle, also marks the point (B) where the curved region and conical region meet. The maximum deviation of the conical region from the $1$ radian angle is a mere $37~\mu m$.
As we will see later, this $1$ radian arc is also used to position and dimension the handles.
The $R(n)$ function, discussed above, still leaves a few circular features unaccounted for, so let us explore how these were dimensioned. The opening into the internal cavity of the object has an interesting feature, in that it tapers slightly inward to a point, and then slightly outward again, before blending with the rest of the internal cavity.
Even this extremely delicate feature is perfectly described by the curvature of an $R(6)$ circle. Though the curvature is very slight, it is sufficient to create a clearly defined minimum for the internal radius of the opening $(Ri)$. Likewise, an external maximum diameter $(Do)$ is clearly definable from the curvature on the lip exterior.
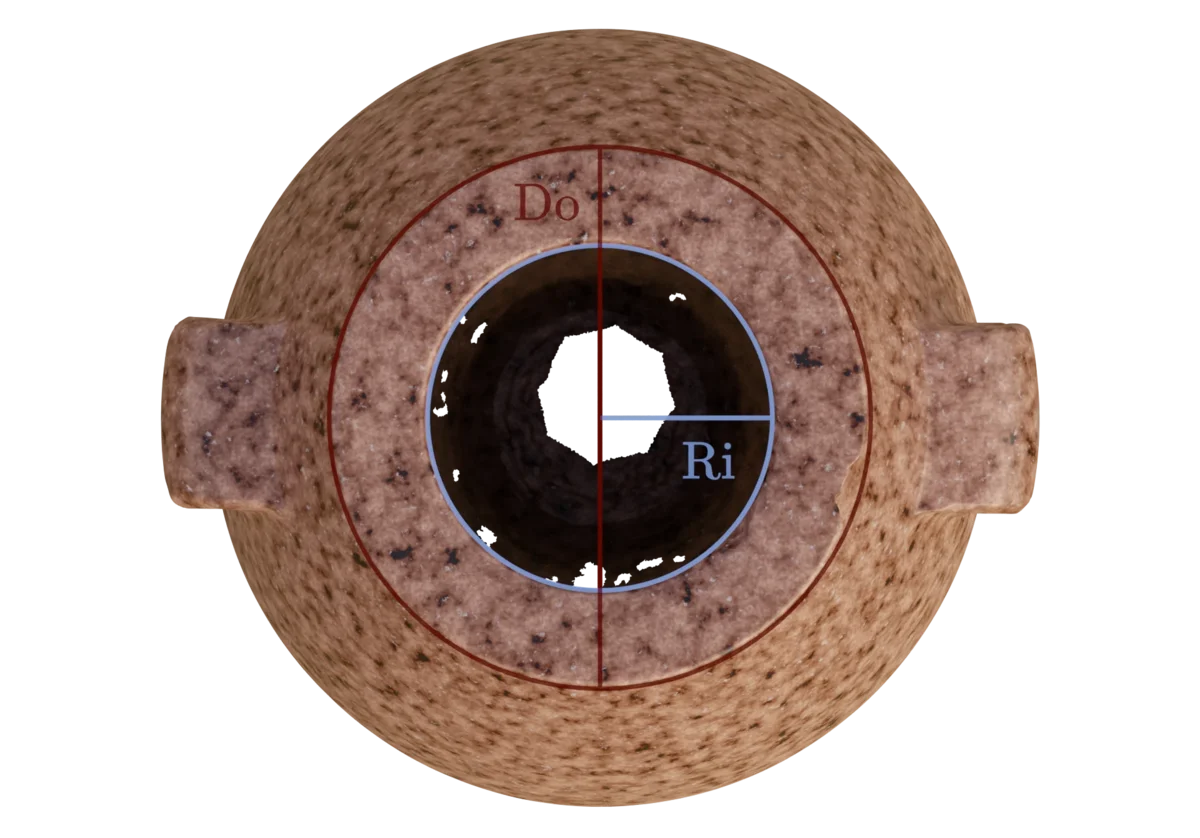
As we can see, the difference between the ratio existing in the physical object, and a perfect representation of $\pi$ is less than $0.11\%$. In such a small object, this equates to a real-world deviation of approximately $32~\mu m$. This finding is also in agreement with observations made by Marián Marčiš. Furthermore, Marián Marčiš has also found preliminary evidence of the same ratio incorporated in an object currently displayed at the Cario Museum.
Here is an experiment to do at home: Try setting a variable gauge to a gap of $32~\mu m$. You will hardly be able to see light pass through that slit. A human hair is twice as thick as the deviation of the $\pi$ ratio in the object. Even calling this an "imperfection" would seem just slightly arrogant.
The creators of this object inscribed $\pi$ to perfection at the microscopic scale, in one of the hardest and most difficult materials to work with. I remain doubtful, that it would even be possible to replicate this result with modern CNC machinery.
In a similar fashion to the use of $\pi$ above, the golden ratio has also been incorporated in the design of the object. The ratio between the diameter of the narrowest part of the exterior neck $(Dn)$, and the inner radius $(Ri)$ is $\varphi^2$.
Again we see a level of precision, that I have a hard time describing with words, so I will let the calculations speak for themselves. In the physical object, this absolutely miniscule deviation from mathematically perfect equates to approximately $20~\mu m$. As with the incorporation of $\pi$, this finding is also in agreement with observations made by Marián Marčiš.
We also find the golden ratio encoded in the ratio between the outer diameter of the lip $(Do)$ and the radius of the foot $(Rf)$:
The deviation in absolute measurements here is approximately $35~\mu m$.
As a sort of mathematical gift, the designers of the object placed a double equivalence here: Since $Do$ is already produced by $\pi$, the radius of the foot can be more purely described as $Rf = {Ri \times \pi \over \varphi^2}$. Because this creates an equivalence between all four measures, established by fundamental mathematical concepts, the following should be a reasonable extension:
I really cannot imagine a more elegant and beautiful way to establish and communicate a base unit of measure. Whoever created this fascinating object wanted us to know what their measurement system looked like, and here it is. Set in stone, in the universal language of mathematics, and preserved through the ages. Absolutely incredible.
Since we do not currently have any better designation, we will refer to the unit of measure used in the design as $U$ (Units). According to our measurements, an approximation to this unit of measure could be:
Since we have observed dimensional deviations of between $20\mu m$ and $32\mu m$ in the measurements used to arrive at this number, we do not recommend using the above approximation as a basis for reference outside of this article.
We do, however, see an interesting corellation in this number. The approximation we have arrived at is just a mere $2.07\mu m$ (less than the scan accuracy) away from exactly matching the wavelength of an eloctromagnetic wave, with a frequency of $16~GHz$, propagating in vacuum:
We believe this establishes a more clear common reference, since $1~U$ can elegantly be defined as a simple subdivison of the speed of light in a vacuum.
For the purpose of having a shared reference, and thus the ability to talk about this unit without undue confusion, we would like to humbly propose its provisional definition based on the above ratio:
With the above information, we are now able to see what the dimension of this object would really have looked like to its creators. Millimeters have a hard time conveying any meaning here, but once we view the dimensions in $U$, we are treated to a very different, and beautiful picture:
| Dimension | $U$ | $mm$ |
|---|---|---|
| Opening Radius | $1$ | $~18.74$ |
| Height | $32 \over 5$ | $~119.9$ |
| Width | $9 \over 2$ | $~84.3$ |
| Width at Handles | $46 \over 9$ | $~95.7$ |
| Max Lip Diameter | $\pi$ | $~58.9$ |
| Min Neck Diameter | $\varphi^2$ | $~49.0$ |
| Foot Radius | ${\pi \over \varphi^2}$ | $~22.5$ |
In this section, we will show how the handles are created. The mathematics needed for this willl get a little more complex, and may not be interesting for everyone. However, we believe it is very important to account for this construction clearly, since it shows with undeniable clarity, just how complex and interrelated the design of the object is, and we want to present the mathematics as a concrete proof for this.
If you are not interested in the equations, you can skip to immediately after the vector construction, where we will return to talking about what it means, in plain english.
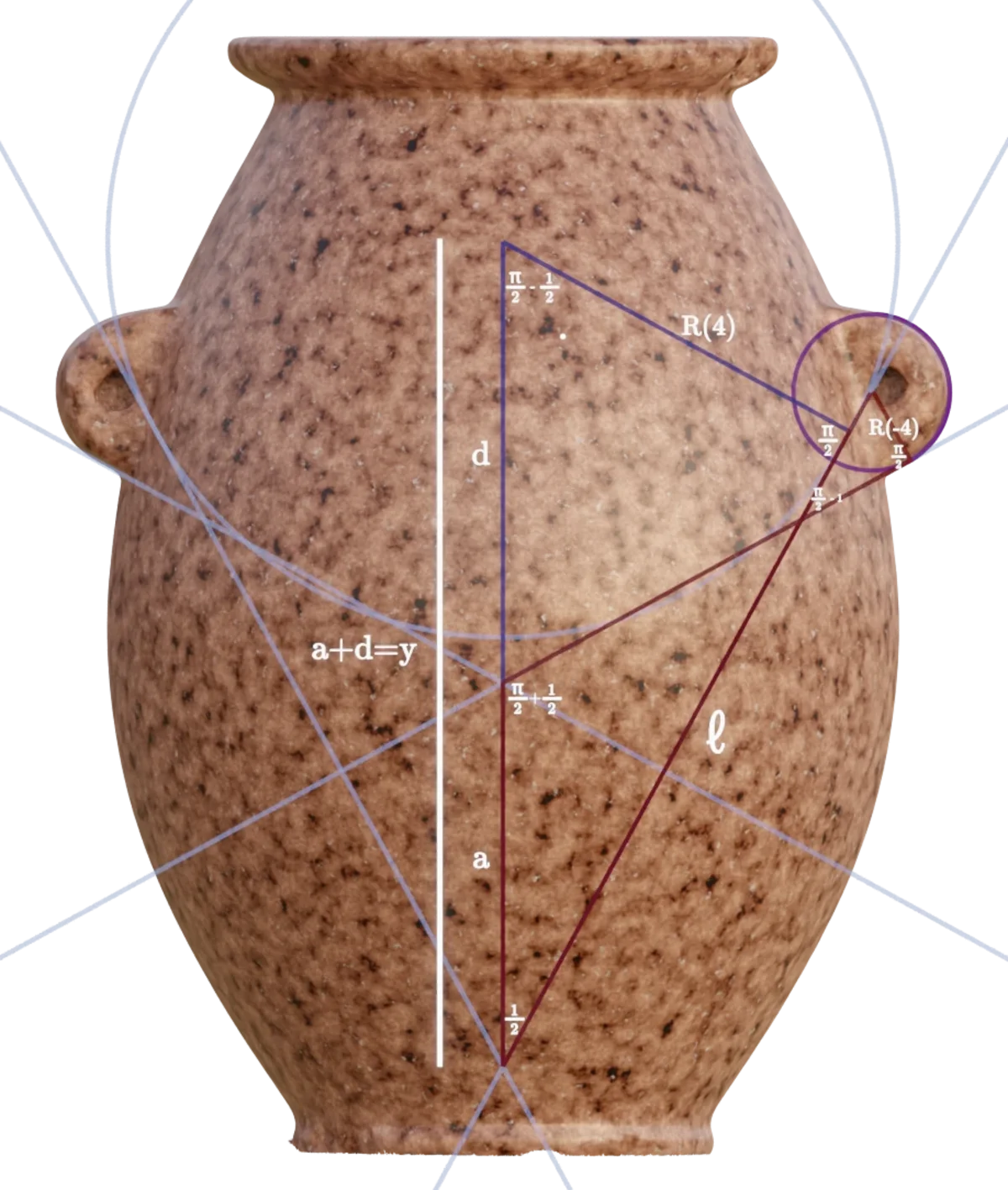
The geometry of the handles is constructed from an interaction between two of the 1 radian arcs, introduced earlier. The first of these arcs is extended from the center intersection point of the R(3) Flower Of Life grid:
The second is created by constructing a $1$ radian arc, that is tangent to the upper circle in the $R(4)$ Flower Of Life grid:
With these two arcs defined (originating from the $R(3)$ and $R(4)$ Flower Of Life grids), and an $R(-4)$ circle, we now have all the constraints necessary to construct the geometry of the handles, which can be expressed as a polar vector, $V_h$:
The remaining features of the handles are accounted for as follows:
We have not been able to simplify this construction any further than the above, and believe it is most likely the optimal configuration for creating the handles, in terms of simplicity. The implications of this are substantial.
The physical geometry, that we observe in the finished object, is essentially created as the solution to a highly interrelated set of equations, that span the entire object, in multiple dimensions and configuration spaces.
We consider it highly likely that the entire object can indeed be represented as a single equation.
It is our conviction that our current model demonstrates, with overwhelming certainty, that a high degree of sophisticated design principles, and intricately interlinked relations and design constraints are present in the object.
While we cannot tell with certainty, if the way that we have described the design exactly matches that of the original creators, we are confident that our reverse-engineered model does indeed represent the actual mathematics, interrelations and constraints present in the original design.
While there is still much to learn about this fascinating artefact, the knowledge and data we already have, allows us to draw some conclusions with confidence.
Could an object like this simply have been a chance happening? A rare coincidence of random alignment?
No. Proposing that would be completely magical and superstitious thinking.
Maintaining absolute precision and consistency by chance, between all the interlinked systems present in the object, is - simply put - an impossibility. Waking up one morning, with an entirely new universe sprouting from quantum fluctuations in your left nostril, would be a significantly more likely event.
It might be possible, by extreme luck to have an object randomly show the value of $\pi$ or $\varphi$ somewhere, but remember that all systems in this object are tightly interrelated! Changing one parameter would throw everything else off. Here, at least 15 levels of interrelation exists, and they are all precisely in harmony, down to microscopic scales.
This object was meticulously and carefully designed by a human being, with incredible levels of skill, insight and artistry. Of that, there can currently be no doubt.
What kind of system would have been necessary to represent the abstract design of the object, before its manufacture? Could the object have been designed by analogue means, for example as a drawing on paper, which was then used to guide the manufacture?
To attempt a satisfactory answer to this question, we will need to carefully consider a multitude of factors. A future article will delve into the full depth, that this question deserves, but we feel that our initial conclusions on the matter still bear touching upon here, even if only briefly.
When looking at the scales across which precision was maintained in this object, some interesting problems arise. The smallest radii - identified so far - in the object are only around $1 mm$, but they scale perfectly, through the radial traversal function, with precision in the micrometers, to even the largest radii in the object (of around $63mm$).
Carrying out this sort of scaling on any kind of analogue medium, would introduce errors immediately, that would only accumulate over successive radial traversals. Even our modern, finely tipped drawing tools, working on the smoothest of paper would create errors close to the full radii of some of these circles and features.
To account and control for such errors, the designer would have to scale up the blueprint to proportions of at least several meters, which of course just raises further questions of how to transfer it back down again, to the decidedly petite dimensions of the actual object.
Perhaps the most plausible way to represent this object on an analogue medium, would be to describe it geometrically and mathematically. This is decidedly possible, and one could even make sketches along the way, to show an approximation of the final design. Our civilization has known about the required mathematics to do this since approximately 500 CE.
But being faced with the prospect of then transferring this design through a manufacturing process, to a physical object, we are put squarely back to the starting point, since we now need to produce some sort of analogue template that can guide or control the manufacturing process.
While the point I will now make certainly necessitates a full, and very formal substantiation, I feel it would simply be cowardly of me, not to bring this argument to its logical conclusion, and stand by where the evidence and logic leads.
As far as we know, no human beings, trained animals or naturally occurring phenomenae, modern or ancient, take mathematical formulae and equations as input, and produce lathe-operating motions as outputs.
For all of the knowledge and insights we have accumulated over the ages, we know of exactly one, and only one category of things capable of such behaviour: The kind of thing, that we refer to as a turing machine. A device capable of taking input, holding state, performing operations on held states, according to pre-determined principles, and producing output.
They come in many shapes and sizes, and can be constructed mechanically, electronically and even pneumatically or hydraulically. And you are most likely using one right now, to read this article.
We call this class of device a computer, and no plausible way of representing, operating on, or manufacturing the design of this artefact exists, without having access to one such.
When comparing the output of our generative model to the physical object, we can begin to get some rough insights into the fabrication capabilities of the creators of the object. From only looking at the observable facts, we can conclude the following:
Based on the best understanding we currently have of the object, and on the knowledge of normal fundamental limits of physics and laws of nature, we have to conclude:
There is no way, in which we can attribute the production of this artefact, to anyone who do not possess, at minimum, the level of technological sophistication and capabilities mentioned above. This raises some very interesting questions regarding the origin of the object, which we hope to be able to explore in future work.
We hope that a number of similar objects (of which there are thousands, in museums around the world) can be scanned with the same, or better, scanning technology, so that a body of work can be built up around the analysis of these remarkable artefacts.
With the analytical tools and technologies we have available today, we stand at the beginning of a new era of inquiry into our past and shared heritage. I can imagine few things more valuable, than deepening the understanding of our collective origins, as a species, and as individuals.
Only by open, critical and honest scientific inquiry, working from first principles anchored in concrete and verifiable data, can the deepest and most obscured echoes of our shared past be brought into the light of day once more.
We must allow the observable facts, the givens that we have, to speak without prior interpretation, even if the conclusions risk temporarily upsetting a prior understanding.
In the scientific endeavour, all theories are provisional, and must yield when a simpler one, that better fits the evidence, can be constructed. If this fundamental tenet ceases to hold primacy, science ceases to be science, and instead degrades into dogma.
